Pages created and updated by Terry Sturtevant Date Posted: June 5, 2017

Maxima Tutorial

Maxima is a GPL program, available for Windows, Mac, and Linux. It is a computer algebra system (CAS) like Maple or Mathematica.
There are various tutorials out there on how to use Maxima; this one is designed to focus on its use for circuit analysis; i.e. lots of use of Kirchhoff's Laws, and including complex numbers for AC analysis with capacitors and inductors.

Sample DC Circuit

Here is a simple circuit:

sample circuit

It gives us the following three Kirchhoff's Law equations ( See the complete analysis here. ) :
-I1 R1 + I3 R3 = -V1

-I2 R2 -I3 R3 = -V2

-I1 + I2 -I3 = 0

A computer algebra system can be very useful for analyzing circuits like this.

  1. Opening Maxima

  2. Solving Equations

  3. Saving a Session

  4. Quitting Maxima

  5. Loading a Previous Session

  6. Redefining Variables

  7. Getting Resistor Voltages

  8. Phasors and AC Circuits (external document)

  9. Links

  1. Opening Maxima:
    • At a command prompt, type maxima 
      bash-4.1$ maxima
Maxima 5.25.1 http://maxima.sourceforge.net
using Lisp CLISP 2.49 (2010-07-07)
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
The function bug_report() provides bug reporting information.
(%i1)


  2. Solving Equations:
    • To solve a set of Kirchhoff's Law equations, use the solve command, solving for I1, I2, and I3:

      At the prompt, type in the the command as shown: 
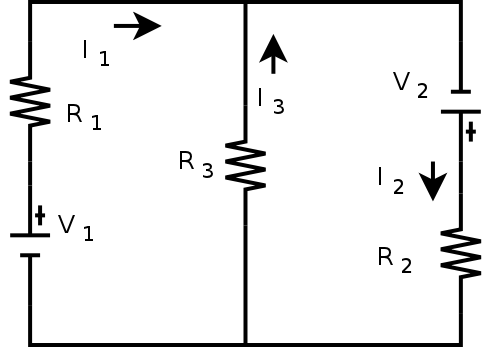
      (%i1) solve([-i_1*r_1+i_3*r_3=-v_1,
-i_2*r_2-i_3*r_3=-v_2,
-i_1+i_2-i_3=0
], [i_1,i_2,i_3]);
              r_3 v_2 + (r_3 + r_2) v_1        r_3 v_2 + r_1 v_2 + r_3 v_1
(%o1) [[i_1 = -------------------------, i_2 = ---------------------------, 
              (r_2 + r_1) r_3 + r_1 r_2         (r_2 + r_1) r_3 + r_1 r_2
                                                        r_2 v_1 - r_1 v_2
                                            i_3 = - -------------------------]]
                                                    (r_2 + r_1) r_3 + r_1 r_2
      The solve command usually gives a set of solutions to a single function, so by making the set of equations into a vector, then the solution becomes a single vector.

    • The solution is a vector (of one element) since there is one solution. We can pick off this element, by using the index of the previous result: 
                    r_3 v_2 + (r_3 + r_2) v_1        r_3 v_2 + r_1 v_2 + r_3 v_1
(%o1) [[i_1 = -------------------------, i_2 = ---------------------------, 
              (r_2 + r_1) r_3 + r_1 r_2         (r_2 + r_1) r_3 + r_1 r_2
                                                        r_2 v_1 - r_1 v_2
                                            i_3 = - -------------------------]]
                                                    (r_2 + r_1) r_3 + r_1 r_2
(%i2) %o1[1];
             r_3 v_2 + (r_3 + r_2) v_1        r_3 v_2 + r_1 v_2 + r_3 v_1
(%o2) [i_1 = -------------------------, i_2 = ---------------------------, 
             (r_2 + r_1) r_3 + r_1 r_2         (r_2 + r_1) r_3 + r_1 r_2
                                                         r_2 v_1 - r_1 v_2
                                             i_3 = - -------------------------]
                                                     (r_2 + r_1) r_3 + r_1 r_2
      This ability to recall previous results is very useful, and we'll use it a lot.

    • This looks much the same, although if you look closely you'll see one level of brackets is gone. That's because we're now looking at the first solution, which happens to be the only one in this case.

      We can get an individual current like so: 
                   r_3 v_2 + (r_3 + r_2) v_1        r_3 v_2 + r_1 v_2 + r_3 v_1
(%o2) [i_1 = -------------------------, i_2 = ---------------------------, 
             (r_2 + r_1) r_3 + r_1 r_2         (r_2 + r_1) r_3 + r_1 r_2
                                                         r_2 v_1 - r_1 v_2
                                             i_3 = - -------------------------]
                                                     (r_2 + r_1) r_3 + r_1 r_2
(%i3) %o1[1][1];
                              r_3 v_2 + (r_3 + r_2) v_1
(%o3)                   i_1 = -------------------------
                              (r_2 + r_1) r_3 + r_1 r_2
      (In other words, we're selecting the 1st element of the first solution vector.)

    • We can get the voltage across a resistor by multiplying the current times the resistance, and assigning it to a new variable: 
      (%i3) %o1[1][1];
                              r_3 v_2 + (r_3 + r_2) v_1
(%o3)                   i_1 = -------------------------
                              (r_2 + r_1) r_3 + r_1 r_2
(%i4)  v_r1: %o3*r_1; 
                             r_1 (r_3 v_2 + (r_3 + r_2) v_1)
(%o4)              i_1 r_1 = -------------------------------
                                (r_2 + r_1) r_3 + r_1 r_2

    • You can substitute in specific component values: 
      (%i4)  v_r1: %o3*r_1; 
                             r_1 (r_3 v_2 + (r_3 + r_2) v_1)
(%o4)              i_1 r_1 = -------------------------------
                                (r_2 + r_1) r_3 + r_1 r_2
(%i5) %o1,v_1=5,v_2=12,r_1=1000,r_2=2700,r_3=4300;
                          433          851              3
(%o5)            [[i_1 = -----, i_2 = ------, i_3 = - -----]]
                         93050        186100          37220


  3. Saving a Session:
    • Saving a session: (The "all" means to save all variables from this session.) 
      (%i5) %o1,v_1=5,v_2=12,r_1=1000,r_2=2700,r_3=4300;
                          433          851              3
(%o5)            [[i_1 = -----, i_2 = ------, i_3 = - -----]]
                         93050        186100          37220
(%i6) save("test",all);
(%o6)                       /home/terry/maxima/test


  4. Quitting Maxima:
    • Quitting maxima: 
      (%o6)                       /home/terry/maxima/test
(%i7) quit();


  5. Loading a Previous Session:
    • It's nice to be able to pick up where you left off, so you can keep developing an analysis over time.
      To loading a previous session: 
      bash-4.1$ maxima
Maxima 5.25.1 http://maxima.sourceforge.net
using Lisp CLISP 2.49 (2010-07-07)
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
The function bug_report() provides bug reporting information.
(%i1) load("test");
(%o6)                                test
      Notice that the statement number has jumped ahead; all of the statements from the previous session have been included in this one.

    • Previous statements can be recalled: 
      (%i1) load("test");
(%o6)                                test
(%i7) %o1;
              r_3 v_2 + (r_3 + r_2) v_1        r_3 v_2 + r_1 v_2 + r_3 v_1
(%o7) [[i_1 = -------------------------, i_2 = ---------------------------, 
              (r_2 + r_1) r_3 + r_1 r_2         (r_2 + r_1) r_3 + r_1 r_2
                                                        r_2 v_1 - r_1 v_2
                                            i_3 = - -------------------------]]
                                                    (r_2 + r_1) r_3 + r_1 r_2

(%i8) %o5;
                          433          851              3
(%o8)            [[i_1 = -----, i_2 = ------, i_3 = - -----]]
                         93050        186100          37220


    • Statements can be re-evaluated with different numbers: 
      (%o8)            [[i_1 = -----, i_2 = ------, i_3 = - -----]]
                         93050        186100          37220

(%i9) %o1, v_1=5, v_2=12, r_1=1e3, r_2=2.7e3, r_3=4.3e3;
(%o9) [[i_1 = .004653412144008598, i_2 = .004572810317033852, 
                                                 i_3 = - 8.060182697474475E-5]]


      If numbers are not integers, results will also be non-integer
      Note that as soon as we use scientific notation, values become non-integer.

  6. Redefining Variables:
    • Variables can be changed: 
      (%o9) [[i_1 = .004653412144008598, i_2 = .004572810317033852, 
                                                 i_3 = - 8.060182697474475E-5]]
 (%i10) %o1,  r_1=z_1, r_2=z_2, r_3=z_3;
               v_1 (z_3 + z_2) + v_2 z_3        v_2 z_3 + v_1 z_3 + v_2 z_1
(%o10) [[i_1 = -------------------------, i_2 = ---------------------------, 
               (z_2 + z_1) z_3 + z_1 z_2         (z_2 + z_1) z_3 + z_1 z_2
                                                        v_1 z_2 - v_2 z_1
                                            i_3 = - -------------------------]]
                                                    (z_2 + z_1) z_3 + z_1 z_2


  7. Getting Resistor Voltages:
    • We can pick off individual current equations as well as just the results for each current: 
                     v_1 (z_3 + z_2) + v_2 z_3        v_2 z_3 + v_1 z_3 + v_2 z_1
(%o10) [[i_1 = -------------------------, i_2 = ---------------------------, 
               (z_2 + z_1) z_3 + z_1 z_2         (z_2 + z_1) z_3 + z_1 z_2
                                                        v_1 z_2 - v_2 z_1
                                            i_3 = - -------------------------]]
                                                    (z_2 + z_1) z_3 + z_1 z_2
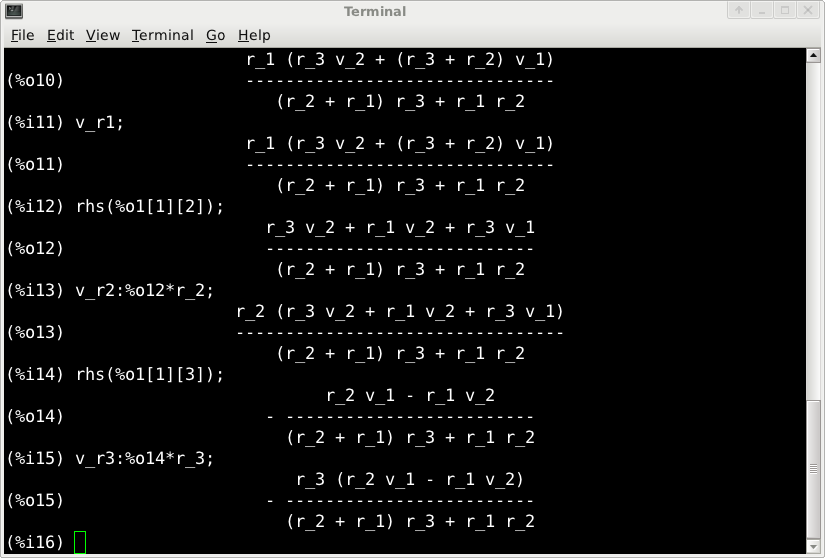
(%i11) rhs(%o1[1][1]);
                           r_3 v_2 + (r_3 + r_2) v_1
(%o11)                     -------------------------
                           (r_2 + r_1) r_3 + r_1 r_2


    • We started to calculate resistor voltages earlier, but we can still do that:
      We had 
                                    r_3 v_2 + (r_3 + r_2) v_1
(%o3)                   i_1 = -------------------------
                              (r_2 + r_1) r_3 + r_1 r_2
(%i4)  v_r1: %o3*r_1; 
                             r_1 (r_3 v_2 + (r_3 + r_2) v_1)
(%o4)              i_1 r_1 = -------------------------------
                                (r_2 + r_1) r_3 + r_1 r_2
      so we can do this: 
      (%i12) %o4,v_1=5,v_2=12,r_1=1000,r_2=2700,r_3=4300;
                                           8660
(%o12)                           1000 i_1 = ----
                                           1861
      This may look odd at first, but realize that the right hand side of the equation gives the value of VR1.
      We could have done this instead: 
      (%i13) v_r1,v_1=5,v_2=12,r_1=1000,r_2=2700,r_3=4300;
                                           8660
(%o13)                           1000 i_1 = ----
                                           1861
      since we defined VR1 as a variable in %i4.

    • It should be obvious how to get VR2 and VR3 :
      getting other resistor voltages

  8. Phasors and AC Circuits (external document)

  9. Links:
    • Maxima Manual [HTML; ]
      The official documentation
    • Maxima Overview [HTML; Burkhard Bunk]
      A good shorthand reference to commands and syntax
    • Maxima tutorial [HTML; Boris Gaertner]
      The "First Steps" and "Getting Started" sections are very useful introductions to the basics.

Creative Commons License
Information on this site which is produced by Terry Sturtevant is licensed under a
Creative Commons Attribution-Noncommercial-Share Alike 2.5 Canada License.

Resources

To view pdf documents, you can download Adobe Acrobat Reader .
get Acrobat Reader
If you need to update a browser, you might try Firefox which is Get Firefox!
Since this page uses cascading style sheets for its layout, it will look best with a browser which supports the specifications as fully as possible.

If you are looking for an office package, with a word processor, spreadsheet, etc., you might try LibreOffice which is Get LibreOffice!

Go to the main page for the Department of Physics and Computer Science.

Valid XHTML 1.1

Valid CSS!

WCAG 2.0 (Level AA)

Wilfrid Laurier University

© 2019 Wilfrid Laurier University