Pages created and updated by Terry Sturtevant Date Posted: June 6, 2017

Maxima Tutorial: Phasors and AC Circuits

Maxima is a GPL program, available for Windows, Mac, and Linux. It is a computer algebra system (CAS) like Maple or Mathematica.
There are various tutorials out there on how to use Maxima; this one is designed to focus on its use for AC circuit analysis; i.e. the use of complex numbers for AC analysis with capacitors and inductors.

Sample AC Circuit

A basic example of the use of phasors is the investigation of simple series and parallel LC circuits. For ideal components,
Z_L= I ω L
and
Z_C= 1/ (I ω C )
Here are simple series and parallel LC circuits:





A computer algebra system can be very useful for analyzing circuits like this.

1. Opening Maxima

2. Defining Impedances

3. Series Circuit Properties

4. Parallel Circuit Properties

---

1. Opening Maxima:
   • At a command prompt, type maxima

     bash-4.1$ maxima
     Maxima 5.25.1 http://maxima.sourceforge.net
     using Lisp CLISP 2.49 (2010-07-07)
     Distributed under the GNU Public License. See the file COPYING.
     Dedicated to the memory of William Schelter.
     The function bug_report() provides bug reporting information.
     (%i1) 
     

2. Defining Impedances
   • It is quite useful to not have to specify component values at the beginning, because the results can be determined algebraically once, after which it is only necessary to substitue in specific quantities.

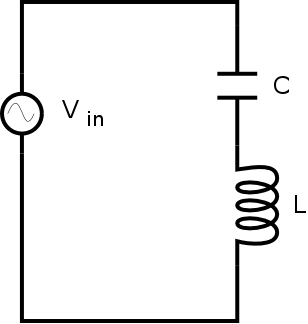
     (%i1)   z_l: %i * omega * L;
     
     (%o1)                             %i L omega
     

     
     

     (%i2)   z_c: 1/( %i * omega * C);
     
                                            %i
     (%o2)                              - -------
                                          C omega
     

     
     
3. Series Circuit Properties
   • The impedance of an LC circuit is easy to check in 3 specific situations;
     the high frequency limit,
     the DC frequency limit,
     the resonant frequency, where ω = 1/√ LC 
     

     (%i3)   z_s: z_l + z_c;
     
                                                 %i
     (%o3)                        %i L omega - -------
                                               C omega
     

     
     Limits are useful for testing the high frequency case:
     

     (%i4)   limit(z_s,omega,infinity);
     
     (%o4)                              infinity
     

     
     Limits can also be used for the low frequency case:
     

     (%i5)   limit(z_s,omega,0);
     
     (%o5)                              infinity
     

     
     Finding the value at the resonant frequency can be done by substituting the value for ω:
     

     (%i6)   ratsimp(z_s), omega = 1/sqrt(L*C);
     
     (%o6)                                  0
     

     
     Note: The use of ratsimp allows simplification of the resulting fractions to occur.
     To see the magnitude of a complex quantity, use the cabs function, as in the following:

     (%i7)   cabs(z_s);
     
                                   !             1   !
     (%o7)                         !L omega - -------!
                                   !          C omega!
     

     
     
     To see the phase of a complex quantity, use the carg function, as in the following:

     (%i8)   carg(z_s);
     
                                                  1
     (%o8)                     atan2(L omega - -------, 0)
                                               C omega
     

     
     
4. Parallel Circuit Properties

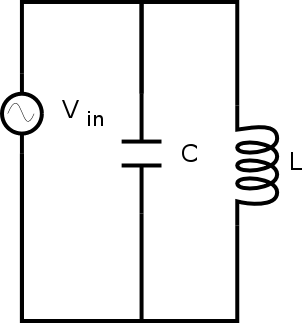
   • (%i9)   z_p: (z_l * z_c)/(z_l + z_c);
     
                                           L
     (%o9)                      ------------------------
                                                  %i
                                C (%i L omega - -------)
                                                C omega
     

     
     The high and low frequency cases can be tested as before:
     

     (%i10)   limit(z_p,omega,infinity);
     
     (%o10)                                 0
     

     
     

     (%i11)   limit(z_p,omega,0);
     
     (%o11)                                 0
     

     
     Since the impedance at the resonant frequency is undefined, the limit has to be used:
     

     (%i12)   limit(z_p, omega, 1/sqrt(L*C));
     
     (%o12)                             infinity
     

     
     

Information on this site which is produced by Terry Sturtevant is licensed under a
Creative Commons Attribution-Noncommercial-Share Alike 2.5 Canada License.