Pages created and updated by Terry Sturtevant Date Posted: June 5, 2017

Maple Kirchhoff's Law Tutorial

Maple is a commercial program. It is a computer algebra system (CAS) like Maxima or Mathematica.
There are various tutorials out there on how to use Maple; this one is designed to focus on its use for circuit analysis; i.e. lots of use of Kirchhoff's Laws, and including complex numbers for AC analysis with capacitors and inductors.

Sample DC Circuit

Here is a simple circuit:



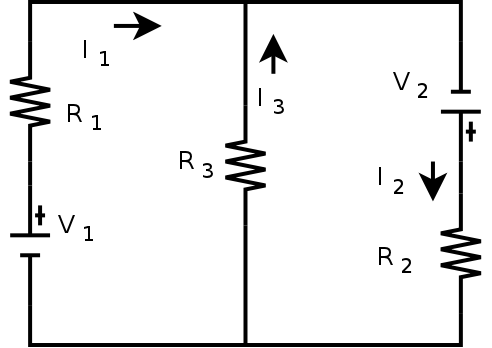
It gives us the following three Kirchhoff's Law equations ( See the complete analysis here. ) :
-I₁ R₁ + I₃ R₃ = -V₁

-I₂ R₂ -I₃ R₃ = -V₂

-I₁ + I₂ -I₃ = 0

A computer algebra system can be very useful for analyzing circuits like this.

1. Opening Maple

2. Solving Equations

3. Saving a Session

4. Quitting Maple

5. Loading a Previous Session

6. Redefining Variables

7. Getting Resistor Voltages

8. Phasors and AC Circuits (external document)

9. Links

---

1. Opening Maple:
   • Open Maple from the menu or the desktop icon.
     
     
2. Solving Equations:
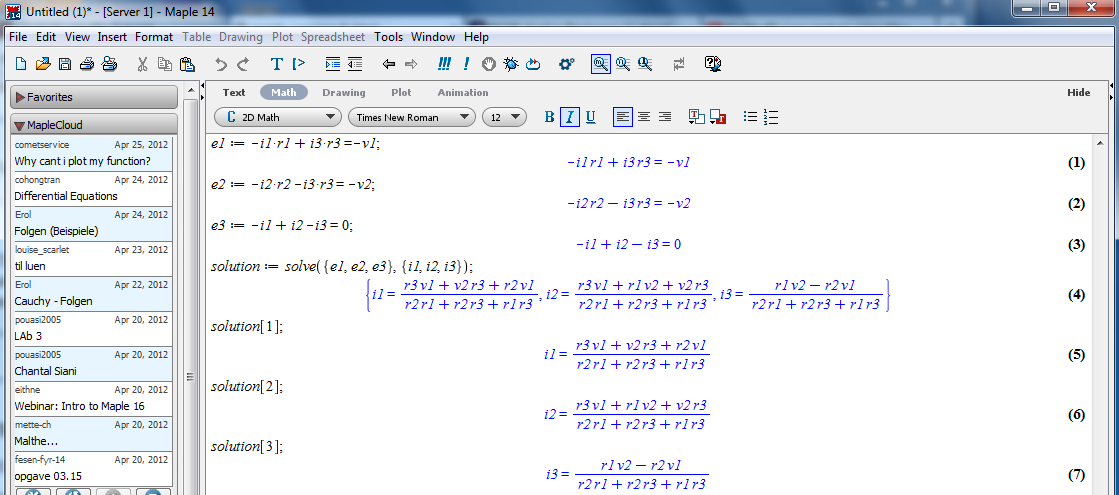
   • To solve a set of Kirchhoff's Law equations, use the solve command, solving for I₁, I₂, and I₃:
     
     At the prompt, type in the the commands as shown:
     
     
     The solve command gives the solution vector.
     
     
     
   • The solution is a vector of currents. We can pick off a single current by using an index with the previous result:
     
     
     
     
   • You can substitute in specific component values:
     
     
     
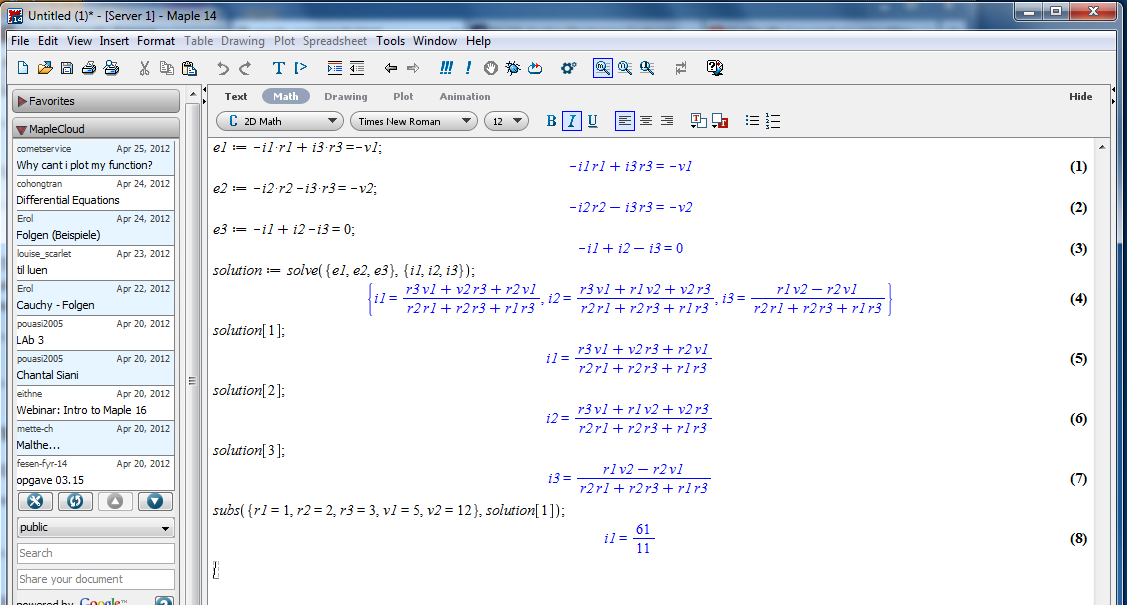
     If numbers are not integers, results will also be non-integer
     Note that as soon as we use scientific notation, values become non-integer.
     
     
   • We can get the voltage across a resistor by multiplying the current times the resistance, and assigning it to a new variable:
     
     
     
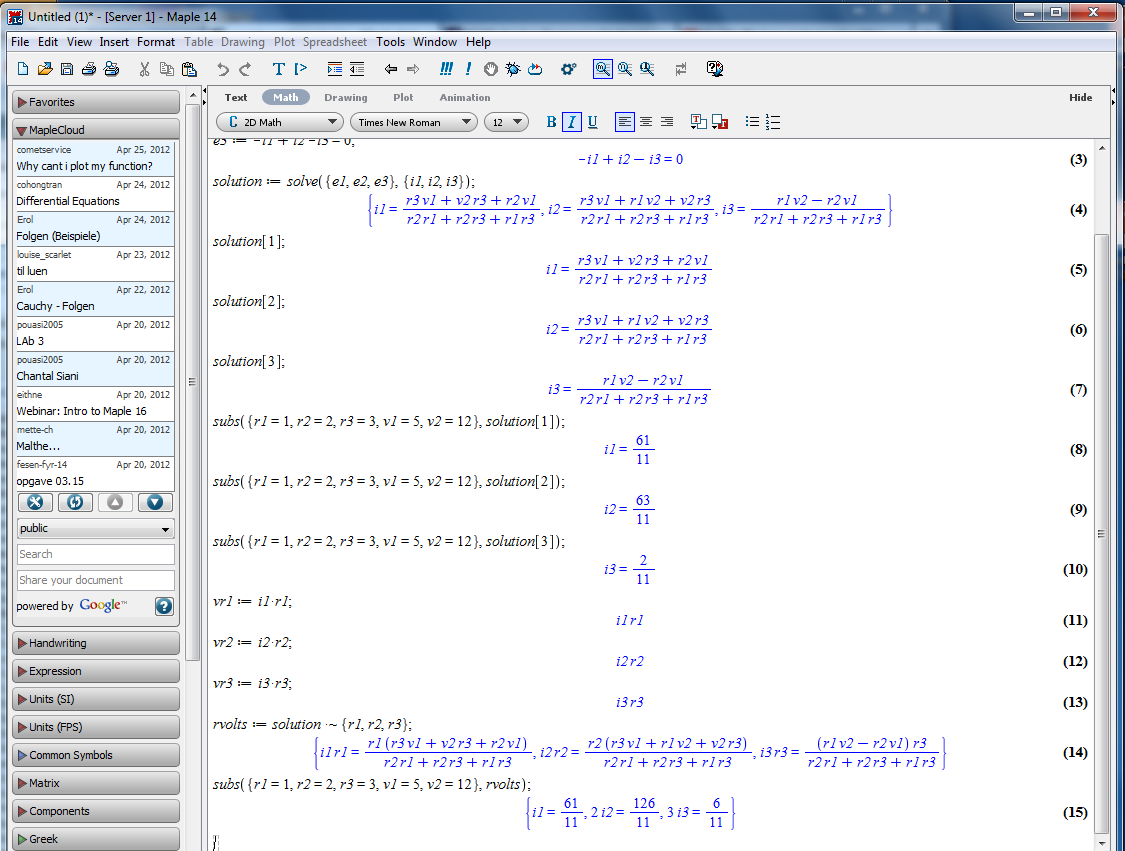
     Important tip: To combine two elements of two different arrays of the same size, just put a tilde after whatever operation you choose (such as +, -, etc.).
     
     
3. Saving a Session:
   • This allows you to come back to it later with all of the variables the same.
     
     To save a session:
     
     
     
     
4. Quitting Maxima:
   • Quitting maxima:
     Choose Exit from the menu.
     
     
5. Loading a Previous Session:
   • It's nice to be able to pick up where you left off, so you can keep developing an analysis over time.
     
     To load a previous session:
     
     
     
     Everything should be as you left it.
     
     
   • Previous statements can be re-executed and/or edited.
     
     
     
   • Statements can be re-evaluated with different numbers.
     
     
6. Redefining Variables:
   • Variables can be changed.
     
     
     
7. Getting Resistor Voltages:
   • We can pick off individual current equations as well as just the results for each current:
     
     
     
8. Phasors and AC Circuits (external document)
   
   
9. Links:
   • Maple Online Help [HTML; ]
     The official online documentation
   • Maple Tutorial [HTML; Texas A & M University]
     Lots of examples

Information on this site which is produced by Terry Sturtevant is licensed under a
Creative Commons Attribution-Noncommercial-Share Alike 2.5 Canada License.