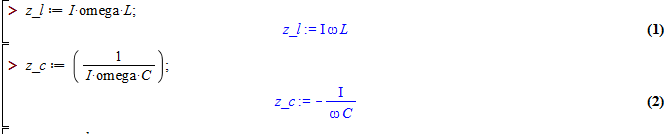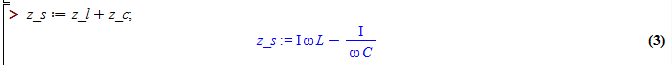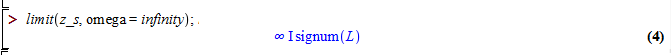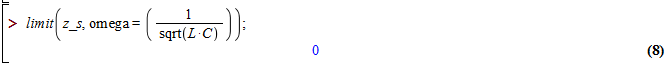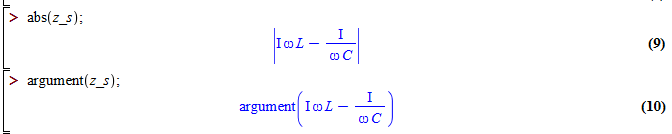Pages created and updated by Terry Sturtevant Date Posted: June 5, 2017

Maple Tutorial: Phasors and AC Circuits

Maple is a commercial program. It is a computer algebra system (CAS) like Maxima or Mathematica.
There are various tutorials out there on how to use Maple; this one is designed to focus on its use for AC circuit analysis; i.e. the use of complex numbers for AC analysis with capacitors and inductors.

Sample AC Circuit

A basic example of the use of phasors is the investigation of simple series and parallel LC circuits. For ideal components,
Z_L= I ω L
and
Z_C= 1/ (I ω C )
Here are simple series and parallel LC circuits:





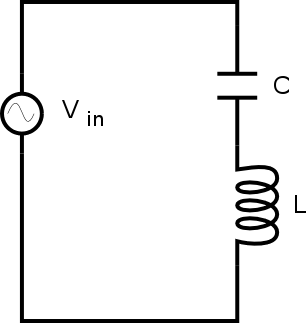
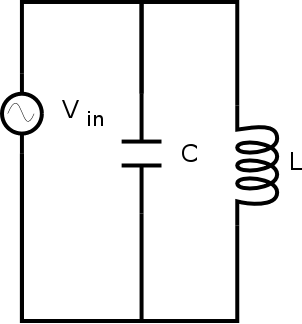
A computer algebra system can be very useful for analyzing circuits like this.

1. Opening Maple

2. Defining Impedances

3. Series Circuit Properties

4. Parallel Circuit Properties

5. Entire Session Transcript

---

1. Opening Maple:
   • Open Maple from the menu or the desktop icon.
     
     
2. Defining Impedances
   • It is quite useful to not have to specify component values at the beginning, because the results can be determined algebraically once, after which it is only necessary to substitue in specific quantities.
     
     
     
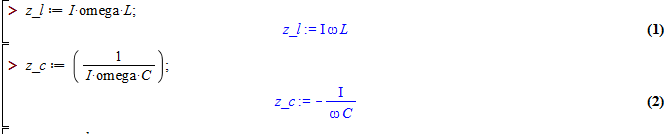
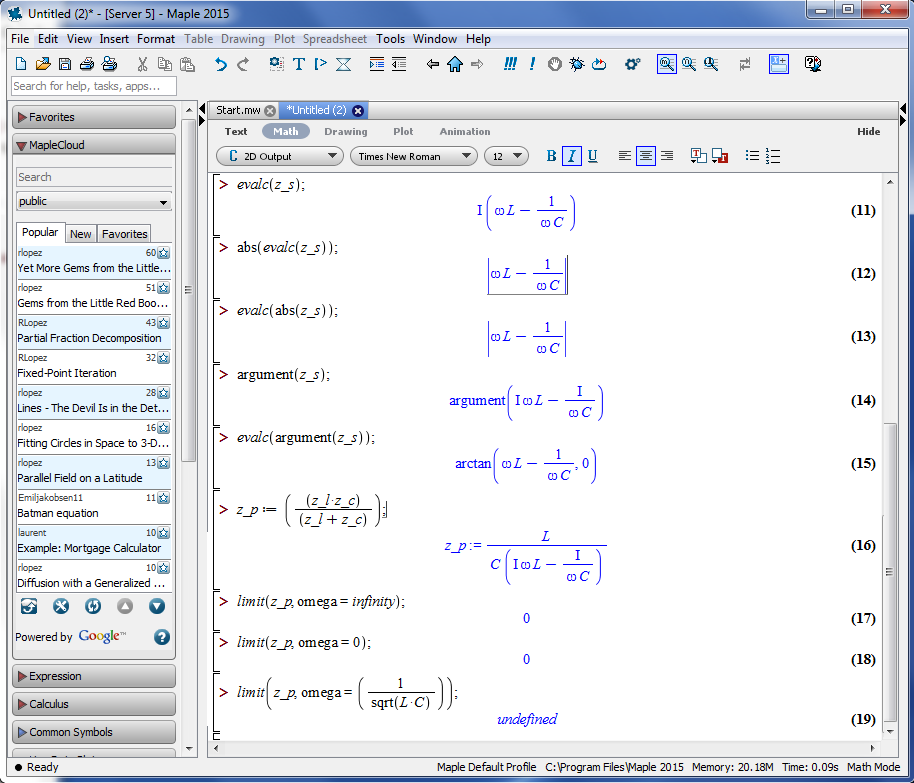
3. Series Circuit Properties
   • The impedance of an LC circuit is easy to check in 3 specific situations;
     the high frequency limit,
     the DC frequency limit,
     the resonant frequency, where ω = 1/√ LC 
     
     
     
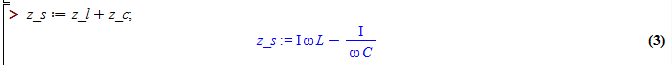
     Limits are useful for testing the high frequency case:
     
     
     
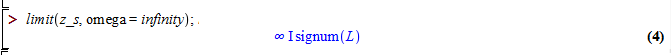
     Note in the high frequency case, where ω goes to infinity, the mathematical result depends on the sign of L; since L can only be positive physically, then this gives the expected result.
     Limits can also be used for the low frequency case:
     
     
     Finding the value at the resonant frequency can be done by using the limit as well:
     
     
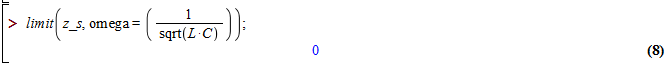
     It can also be found by substitution, as shown in the following:
     
     Note that without using the simplify function, the fact that the result is zero is not immediately apparent.
     
     
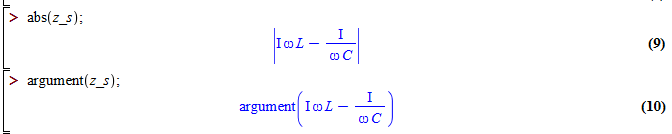
     It's not clear from the above whether the argument function is works, but a further step clarifies it:
     
     The evalc function is for evaluating complex numbers, and taking the absolute value gives the magnitude. (Note the order of abs and evalc doesn't matter.)
4. Parallel Circuit Properties
   • 
     
     The high and low frequency cases can be tested as before:
     
     
     Since the impedance at the resonant frequency is undefined, the limit has to be used.
     
     
5. Entire Session Transcript:
   
   
   
   

Information on this site which is produced by Terry Sturtevant is licensed under a
Creative Commons Attribution-Noncommercial-Share Alike 2.5 Canada License.