CP/PC364 Data Communications & Networks Laboratory

Cyclic Redundancy Check (CRC) adapted from Essaid Bouktache

PRELAB

Overview

CRC code generation is an important tool in computer networking at the data link layer level, since it is at that level that error detection is done by hardware. At a higher layer (transport), error detection is done in software, using a much simpler algorithm to allow speedy processing. In all cases, error detection provides an efficient means of implementing error control for reliable transmission of messages.

Datasheet: 74LS74 [Copyright 1995 National Semiconductor Corporation. Datasheet June 1989]
Datasheet: 74LS86 [Copyright 1995 National Semiconductor Corporation. Datasheet June 1989]
Datasheet: 74LS00 [Copyright 1995 National Semiconductor Corporation. Datasheet June 1989]

Objectives

  1. Generate and receive CRC codes using linear shiftback registers
  2. Verify functionality using polynomial division

Setup

Connect the ByteBlaster cable from the parallel port to your Altera board. Connect power and ground (don't turn on yet.) Open Quartus II on your computer.

Exercise - Part 1

  1. Implement the circuit you just sketched in Quartus II.
  2. Compile.
  3. Simulate. Ensure your design is working properly using the following table.
    Input CLK LED 1 LED 2 LED 3 LED 4
    1 ↑ 1 0 0 0
    1 ↑ 1 1 0 0
    1 ↑ 1 1 1 0
    1 ↑ 1 1 1 1
    1 ↑ 0 0 1 1
    1 ↑ 0 1 0 1
    1 ↑ 0 1 1 0
    1 ↑ 1 0 1 1
    1 ↑ 0 0 0 1
    1 ↑ 0 1 0 0
    1 ↑ 1 0 1 0
  4. Make sure you have your device selected (EPM7064SLC44-10 from the MAX7000S family).
  5. Assign your pins.

    NOTE: If you are selecting the device, or assigning pins for the first time this project compile again before downloading.

  6.   Connect the CPLD and download your program to the board.
  7. Connect 4 LEDS (don't forget resistors) and a signal for your input and the clock.
  8. Test your circuit using the table above.

Exercise - Part 2

  1. Polynomial Arithmetic for CRC Generation
    The CRC, or frame check sequence R, is the remainder of the following binary division: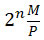 2 to the power n multiplied by M over P. M is a k-bit message, and P is a generating polynomial of degree n. The remainder, R, is then appended to the message M to form a (k + n)-bit frame T to be transmitted.


    Using the mesaage M = 110011101011 from your prelab as an input to your circuit, apply the appropriate number of clock pulses (number of bits in M + n) to generate the CRC code.
    • Compare this result with the CRC code found using polynomial division.
    • Double check your CRC code here: Polynomial Calculator

    Demonstrate and explain your results to the lab instructor.

  2. Clear your circuit so all LEDs are off.

  3. Polynomial Arithmetic for CRC Reception

    At the receiver, the received frame T is divided by the same generating polynomial P. A remainder of 0 indicates no error. Any other remainder is an indication of a burst error. Codes that are generated using shiftback registers and based on generating polynomials can detect 100% of all burst errors up to length n, that is, up to n bits in error, where n is the degree of the generating polynomial P. Higher burst lengths can also be detected, but at a lesser percentage.


    To verify that the circuit is working properly, apply the received frame (frame = M followed by CRC). If your circuit is working properly, the shift register should show all zeros (lights off) at the end of the last clock pulse.

    Demonstrate and explain your results to the lab instructor.

    Part 3

  4. Clear your circuit.
  5. Assume an error burst occurred (within the message bits) so that the message portion of the received frame is Mr = 111100101011 instead of 110011101011. Assume no errors in the received CRC code.
    • Show that your circuit can detect this error, ie the register contents (remainder) should not be zero.
    • Write down the remainder.
    • Perform polynomial division (as in the prelab) and compare with the code shown as your remainder.
  6. Repeat 4 and 5 and introduce two errors in the message portion and two errors in the CRC code of the received frame.

    Demonstrate and explain your results to the lab instructor.

    Part 4

  7. Modify your circuit to use the generating polynomial P(x) = x4 + x3 + 1.
  8. Use the message M = 11100110 and CRC 0110 to transmit the frame T = 111001100110
    • What is your output? Is this what you expect?
  9. Clear your circuit.
  10. Assume an error burst occurred with four errors in the message portion of the received frame and none in the CRC code.
    • Show that your circuit can detect this error, ie the register contents (remainder) should not be zero.
    • Write down the remainder.
    • Perform polynomial division (as in the prelab) and compare with the code shown as your remainder.
  11. Repeat 9 and 10, except, assume four errors in the CRC and none in the message.

    Demonstrate and explain your results to the lab instructor